Tree Traversal — An Informative Guide

Introduction

Tree traversal is the process of visiting all the nodes in a tree data structure in a systematic way. Traversals are fundamental to many algorithms and applications from compilers and file-system operations to search engines and databases. This article explains the core concepts, common traversal strategies, their implementations, time/space complexity, and practical use cases with simple code examples.

What is a tree?

A tree is a hierarchical data structure made of nodes. Each node may have zero or more child nodes. One special node is the root (top), and nodes with no children are leaves. A common example is the binary tree, where each node has at most two children (commonly named left and right).

A tree traversal defines an order in which we visit nodes. Visiting typically means “process the node” e.g., read its value, collect it in a list, or perform computation.

Why traversal matters

• Extracting data in a meaningful order: In-order traversal of a binary search tree yields sorted data.
• Transformations: Converting syntax trees to code or bytecode.
• Searching: Finding a node or checking a property across nodes.
• Serialization & deserialization: Saving and reconstructing trees.
• Resource management: e.g., freeing nodes in the right order.

Main types of tree traversal

1. Depth-First Traversals (DFS)

DFS explores as far down a branch before backtracking. In trees, DFS has three classic orders for binary trees:

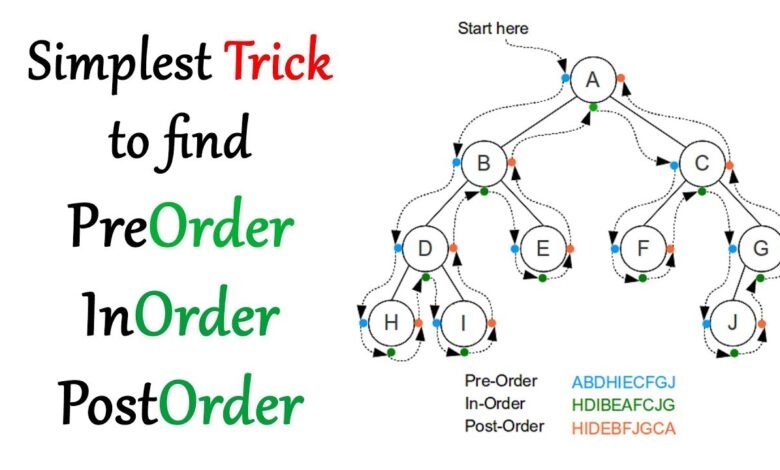
• Preorder (Root, Left, Right)
  Visit the node first, then recursively traverse left subtree, then right subtree.
  Use cases: copy/serialize the tree, prefix notation (Polish notation) for expressions.
• Inorder (Left, Root, Right)
  Traverse left subtree, visit the node, then traverse right subtree.
  Use case: binary search tree (BST) sorted output.
• Postorder (Left, Right, Root)
  Traverse left and right, then visit node.
  Use cases: deleting/freeing nodes, evaluating postfix expressions.

These generalize to non-binary trees by deciding an order among children.

2. Breadth-First Traversal (BFS) / Level-Order

BFS visits nodes level by level from the root downward, left to right within each level (for binary trees). This uses a queue.

Use cases: shortest path in unweighted tree/graph, layout/visualization by level, building level-wise aggregation.

Recursive vs Iterative implementations

Recursive

Recursion naturally follows tree structure and produces concise code. Example (inorder):

def inorder(node):
    if node is None:
        return
    inorder(node.left)
    process(node)
    inorder(node.right)

Pros: simple, easy to read.
Cons: recursion depth equals tree height — risk of stack overflow for very deep trees.

Iterative

Use an explicit stack for DFS, or a queue for BFS. Iterative inorder for binary tree uses a stack to simulate recursion.

Pros: avoids recursion limits, sometimes more control.
Cons: slightly more complex code.

Example code snippets

Binary tree node (Python)

class Node:
    def __init__(self, val, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

Inorder (iterative)

def inorder_iterative(root):
    stack = []
    curr = root
    result = []
    while stack or curr:
        while curr:
            stack.append(curr)
            curr = curr.left
        curr = stack.pop()
        result.append(curr.val)   # process
        curr = curr.right
    return result

Level-order (BFS)

from collections import deque

def level_order(root):
    if not root:
        return []
    q = deque([root])
    result = []
    while q:
        node = q.popleft()
        result.append(node.val)
        if node.left: q.append(node.left)
        if node.right: q.append(node.right)
    return result

Time and space complexity

• Time complexity for any traversal that visits every node once: O(n) where n is the number of nodes.
• Space complexity depends on traversal and tree shape:
  • Recursive DFS: O(h) call stack, where h is tree height (worst-case O(n) for a skewed tree).
  • Iterative DFS with stack: O(h).
  • BFS (level-order): O(w) where w is maximum width (number of nodes at largest level), worst-case O(n) for a broad tree.

Common problems & variations

• Morris traversal (inorder, O(1) extra space) — modifies tree pointers temporarily to traverse without stack/recursion.
• Zigzag (spiral) level-order — alternate left-to-right and right-to-left per level.
• K-ary trees — generalization of binary tree traversal; iterate children in a fixed order.
• Iterative postorder — trickier than preorder/inorder; often done with two stacks or reversed modified preorder.

Practical applications

• Binary Search Trees (BSTs): Inorder traversal yields sorted sequences.
• Expression trees: Preorder gives prefix notation; postorder gives postfix (Reverse Polish) notation for evaluation.
• File systems: Traversing directory trees to list files or compute sizes.
• Compilers: AST (abstract syntax tree) traversals for semantic checks and code generation.
• Search & AI: Tree searches in game trees or decision trees (with different traversal strategies or pruning).
• Serialization: Storing tree structure (e.g., for network transfer) using preorder + null markers or level-order.

Tips & best practices

• Choose inorder for BSTs when you need sorted output.
• Use postorder when child data must be processed before parents (e.g., freeing memory).
• Use level-order when you need the tree organized by levels (e.g., UI rendering, shortest unweighted paths).
• Prefer iterative approach when trees can be very deep to avoid recursion limits.
• Consider Morris traversal if minimizing extra memory is critical and temporary modification is allowed.
• For large scale systems, consider streaming traversal (yielding nodes lazily) to avoid holding full results in memory.

Quick comparison table

Traversal	Order (binary)	Use case	Extra memory
Preorder	Root, Left, Right	Copy tree, prefix notation	O(h) stack
Inorder	Left, Root, Right	BST sorted output	O(h) stack
Postorder	Left, Right, Root	Delete nodes, postfix eval	O(h) stack
Level-order	Level by level	Shortest unweighted paths, UI	O(w) queue

Conclusion

Tree traversal is a core skill for any programmer working with hierarchical data structures. Understanding preorder, inorder, postorder, and level-order and when to use recursive vs iterative implementations gives you powerful tools for solving problems across systems, compilers, databases, and algorithms. Start by practicing simple traversals on small trees, then explore variations like Morris traversal and iterative postorder for deeper mastery.